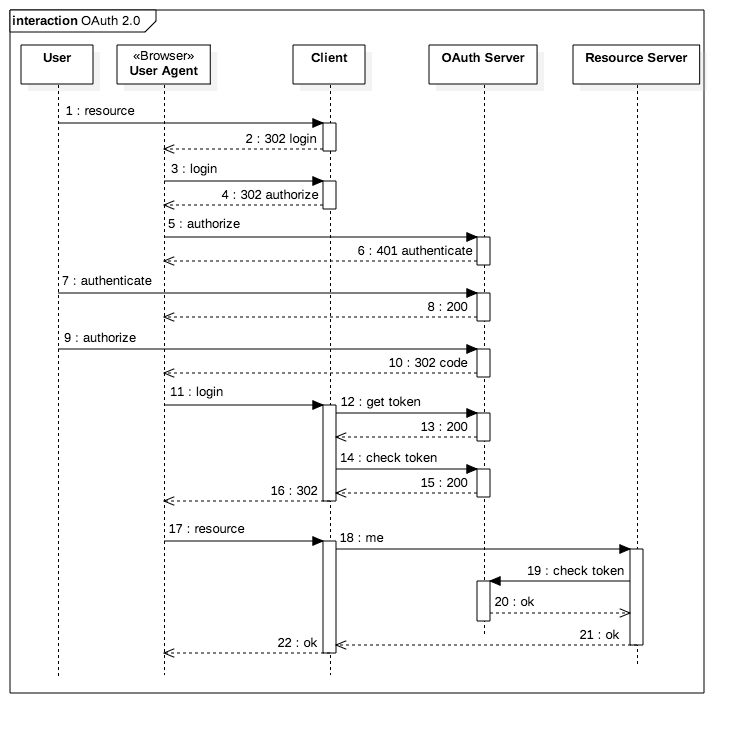
This post is a quick analysis of the Spring implementation of OAuth 2.0 code flow (RFC6749 Section 4.1) with the minumum application code. The setup consists of the authorization server, the resource server, and the client.

The flow starts when a user hits localhost:9999/client/resource

Logistic regression is a classification case of linear regression whith dependent variable $y$ taking binary values.

Problem: Given a training set $\langle x^{(i)}, y^{(i)} \rangle$, $1 \le i \le m$, $x \in \mathbb{R}^{n+1}$, $x^{(i)} _ 0 = 0$, $y^{(i)} \in $ {0,1}, find classification function

$$h_\theta(x) = P(y = 1 | x; \theta)$$

Let $y$ be a dependent variable of a feature vector $x$

$$x = \begin{pmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{pmatrix}$$

Problem: Given a training set $\langle x^{(i)}, y^{(i)} \rangle$, $1 \le i \le m$, find the value of $y$ on any input vector $x$.

We solve this problem by constructing a hypothesis funciton $h_\theta(x)$ using one of the methods below.

In his seminal paper Kenneth Iverson described a new mathematical notation which soon became A Programming Language.

Recently, while reading Surely You’re Joking, Mr. Feynman!, I found that Feynman invented his own notation when he was in school.

Cliff Pickover twitted a fun puzzle: Which series is bigger?

$$\sum_{n=0}^\infty \frac{1}{2^{n+1}} \quad \text{or} \quad \sum_{n=0}^\infty \frac{n}{2^{n+1}}$$

The first one is the famous geometric series which sum is equal to 1. The second one seems to be bigger because 1 < n, except for the 0th term, but that 0th term makes a big difference.