Cryptography Engineering

These are my notes on the book Cryptography Engineering by
Niels Ferguson, Bruce Schneier, Tadayoshi Kohno
Paperback: 384 pages
Publisher: John Wiley & Sons; March 2010
ISBN: 978-0470474242
“The world is full of bad security systems designed by people who have read Applied Cryptography.” Cryptography Engineering could have the same effect.
1. The Context of Cryptography
Every system can be attacked. There is no such thing as perfect security. The whole point of a security system is to provide access to some people and not the others. In the end, you will always have to trust some people in some way, and these pople may still be able to attack your system.
When someone claims that they’ve secured a system against a generic attack, you know to be sceptical.
The best way to have confidence in building something secure is to keep it simple. Complexity is a measure of how many thing interact at any one point. To make a large, simple system you have to provide a very clear and simple interface between different parts of the system. Programmers call this modularization.
2. Introduction to Cryptography
Kerchoffs’ Principle The security of the encryption scheme must depend only on the secrecy of the key, and not on the secrecy of the algorithm.
With enough effort, any practical cryptographic system can be attacked successfully. The real question is how much work it takes to break a system.
3. Block Ciphers
Ideal Block Cipher For each key value, we want the block cipher to be a random permutation, and the different permutations for the different key values should be chosen independently.
A block cipher with a block size of $k$ bits specifies a permutation on $k$-bit output. The maximum key size (in bits) in this case is
For a security level of $n$ bits, every cryptographic value should be at least $2n$ bits long.
Exercise 3.1 How much space would be required to store a table for an entire idealized block cipher that operates on $k$-bit blocks and that has $n$-bit keys?
Exercise 3.2 DES. 64-bit block size; 16 rounds. 56-bit keys. How does 3DES work as a function of DES?
Exercise 3.3 AES. 128-bit block size. Key length, rounds: (128, 10), (192, 12), (256, 14).
Exercise 3.8 Using an existing cryptography library, decrypt the following ciphertext (in hex)
539B 333B 3970 6D14 9028 CFE1 D9D4 A407with the following 256-bit key (also in hex)
8000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001using AES.
8070 6050 4030 2010 0807 0605 0403 0201Solution
$ echo "539B333B39706D149028CFE1D9D4A407" | xxd -r -p | openssl enc -aes256 -d -K "8000000000000000000000000000000000000000000000000000000000000001" -iv 0 -nopad | xxd
Exercise 3.9 Using an existing cryptography library, encrypt the following plaintext (in hex)
296C 93FD F499 AAEB 4194 BABC 2E63 561Dwith the following 256-bit key (also in hex)
8000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001using AES.
8000 0000 0000 0000 0000 0000 0000 0001Solution
$ echo "296C93FDF499AAEB4194BABC2E63561D" | xxd -r -p | openssl enc -aes256 -e -K "8000000000000000000000000000000000000000000000000000000000000001" -iv 0 -nopad | xxd
Exercise 3.10 Write a program that experimentally demonstrates the complementation property of DES.
Solution in Groovy
4. Block Cipher Modes
The encryption modes in this chapter are only designed to provide confidentiality against eavesdroppers; they do not stop the attacker from changing the data.
Any padding scheme is acceptable, as long as it is reversible.
In practice all padding rules add a minimum of one byte to the length of the plaintext.
An erroneous padding should be treated in the same manner as an authentication failure.
All block cipher modes leak some information.
The best you can do at this point is use CTR or CBC and limit the amount of data you process with any one key. We suggest limiting CBC encryption to $2^{32}$ blocks or so, and CTR encryption to $2^{60}$ blocks.
Exercise 4.3 Suppose you, as an attacker, observe a 32-byte ciphertext $C$ and a 32-byte ciphertext $C’$. Suppose you know these ciphertexts were generated using CTR mode with the same nonce. The nonce is implicit, so it is not included in the ciphertext. You also know the plaintext $P$ corresponding to $C$. Then you can derive the plaintext $P’$ corresponding to $C’$
Verification in Groovy
Exercise 4.4 Decrypt the ciphertext (in hex)
87F3 48FF 79B8 11AF 3857 D671 8E5F 0F91
7C3D 26F7 7377 635A 5E43 E9B5 CC5D 0592
6E26 FFC5 220D C7D4 05F1 7086 70E6 E017that was generated with 256-bit AES key (also in hex)
8000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001using CBC mode with a random IV. The IV is included at the beginning of the ciphertext.
416e 6f74 6865 7220 7365 6372 6574 2120 Another secret!
2041 6e64 2061 6e6f 7468 6572 2e20 2020 And another.Solution
$ echo "7C3D26F77377635A5E43E9B5CC5D05926E26FFC5220DC7D405F1708670E6E017" | xxd -r -p | openssl enc -aes-256-cbc -d -K "8000000000000000000000000000000000000000000000000000000000000001" -iv 87F348FF79B811AF3857D6718E5F0F91 -nopad | xxd
Exercise 4.5 Encrypt the plaintext
626c 6f63 6b20 6369 7068 6572 7320 2020 block ciphers
6861 7368 2066 756e 6374 696f 6e73 2078 hash functions x
626c 6f63 6b20 6369 7068 6572 7320 2020 block ciphersusing AES in ECB mode and the key
8000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001Answer
9b75 b376 fdc7 83bd 0dff 4ac4 4078 ea8e .u.v......J.@x..
6655 f422 2c0d 4133 64f7 48e0 8f18 0513 fU.",.A3d.H.....
9b75 b376 fdc7 83bd 0dff 4ac4 4078 ea8e .u.v......J.@x..Solution
$ echo "626C6F636B2063697068657273202020686173682066756E6374696F6E732078626C6F636B2063697068657273202020" | xxd -r -p | openssl enc -aes-256-ecb -e -K "8000000000000000000000000000000000000000000000000000000000000001" -nopad | xxd
Do not ever use ECB for anything.
5. Hash Functions
The collision-resistance requirement merely states that, although collisions exist, they cannot be found.
Some might argue that all $n$-bit hash functions provide only $n/2$ bits of security.
Exercise 5.1 Two blocks
d131 dd02 c5e6 eec4 693d 9a06 98af f95c .1......i=.....\
2fca b587 1246 7eab 4004 583e b8fb 7f89 /....F~.@.X>....
55ad 3406 09f4 b302 83e4 8883 2571 415a U.4.........%qAZ
0851 25e8 f7cd c99f d91d bdf2 8037 3c5b .Q%..........7<[
d882 3e31 5634 8f5b ae6d acd4 36c9 19c6 ..>1V4.[.m..6...
dd53 e2b4 87da 03fd 0239 6306 d248 cda0 .S.......9c..H..
e99f 3342 0f57 7ee8 ce54 b670 80a8 0d1e ..3B.W~..T.p....
c698 21bc b6a8 8393 96f9 652b 6ff7 2a70 ..!.......e+o.*pand
d131 dd02 c5e6 eec4 693d 9a06 98af f95c .1......i=.....\
2fca b507 1246 7eab 4004 583e b8fb 7f89 /....F~.@.X>....
55ad 3406 09f4 b302 83e4 8883 25f1 415a U.4.........%.AZ
0851 25e8 f7cd c99f d91d bd72 8037 3c5b .Q%........r.7<[
d882 3e31 5634 8f5b ae6d acd4 36c9 19c6 ..>1V4.[.m..6...
dd53 e234 87da 03fd 0239 6306 d248 cda0 .S.4.....9c..H..
e99f 3342 0f57 7ee8 ce54 b670 8028 0d1e ..3B.W~..T.p.(..
c698 21bc b6a8 8393 96f9 65ab 6ff7 2a70 ..!.......e.o.*pproduce an MD5 collision
$ echo "d131dd02c5e6eec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f8955ad340609f4b30283e488832571415a085125e8f7cdc99fd91dbdf280373c5bd8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70" | xxd -r | openssl dgst -md5
d41d8cd98f00b204e9800998ecf8427e
$ echo "d131dd02c5e6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f8955ad340609f4b30283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5bd8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0e99f33420f577ee8ce54b67080280d1ec69821bcb6a8839396f965ab6ff72a70" | xxd -r | openssl dgst -md5
d41d8cd98f00b204e9800998ecf8427e
Exercise 5.2 Compute the SHA-512 hash value of the following message in hex:
4865 6C6C 6F2C 2077 6F72 6C64 2E20 2020 Hello, world.Solution
$ echo "48656C6C6F2C20776F726C642E202020" | xxd -r | shasum -ba 512
cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e
Exercise 5.3 Consider SHA-512-n, a hash function that first runs SHA-512 and then outputs only the first $n$ bits of the result. Write a program that uses a birthday attack to find and output a collision on SHA-512-n, where $n$ is a multiple of 8 between 8 and 48. Your program may use an existing cryptography library. Time how long your program takes when $n$ is 8, 16, 24, 32, 40, and 48, averaged over five runs for each $n$. How long would you expect your program to take for SHA-512-256? ($1.5\cdot 10^{26}$ years) For SHA-512-384? ($2.7\cdot 10^{45}$ years) For SHA-512 itself? ($5.0\cdot 10^{64}$ years)
Solution in Groovy.
| Function | Colliding strings (in hex) | Hash (in hex) | Time |
|---|---|---|---|
| SHA-512-8 | 36 / 3130 |
3C |
68ms |
| SHA-512-16 | 313035 / 333732 |
03D2 |
62ms |
| SHA-512-24 | 383938 / 36333138 |
121165 |
157ms |
| SHA-512-32 | 3134313833 / 3933363536 |
2D83D66F |
551ms |
| SHA-512-40 | 343131323130 / 32343433363431 |
5232228D80 |
15sec |
| SHA-512-48 | 37383538363039 / 3132393635383233 |
1A0922E4701D |
233sec |
Exercise 5.4 Let SHA-512-n be as in the previous exercise. Write a program that finds a message $M$ (a pre-image) that hashes to the following values.
| Function | Hash (in hex) | Pre-image (in hex) | Time |
|---|---|---|---|
| SHA-512-8 | A9 |
323030 |
22ms |
| SHA-512-16 | 3D4B |
3931313939 |
633ms |
| SHA-512-24 | 3A7F27 |
3130343632323237 |
2min |
| SHA-512-32 | C3C0357C |
32383732323933353533 |
3hr |
Solution in Groovy
How long would you expect a similar program to take for SHA-512-256? ($8.6\cdot 10^{63}$ years) For SHA-512-384? ($2.9\cdot 10^{102}$ years) For SHA-512 itself? ($9.9\cdot 10^{140}$ years)
Section 5.2.1 Simple but insecure hash function.
Let $K$ be a 256-bit key set to all zeros. To hash the message $m$, first pad it in some way and break it into 128-bit blocks $m_1,…,m_k$. Set $H_0$ to a 128-bit block of all zeros. And now compute $H_i = AES_K(H_{i-1} \oplus m_i)$. Let $H_k$ be the result of the hash function.
Here’s a non-generic attack. Pick a message $m$ such that after padding it splits into two blocks $m_1$ and $m_2$. Let $H_1$ and $H_2$ denote the values computed as part of the hash function’s internal processing; $H_2$ is also the output of the hash function. Now let $m’_1 = m_2 \oplus H_1$ and let $m’_2 = H_2 \oplus m_2 \oplus H_1$, and let $m’$ be the message that splits into $m’_1$ and $m’_2$ after padding.
Exercise 5.5 Show that both $m$ and $m’$ hash to $H_2$
6. Message Authentication Codes
One should never use the same key for both encryption and authentication.
The Horton Principle Authenticate what is meant, not what is said.
Whenever you do authentication, always think carefully about what other information shuold be included in the authentication.
Exercise 6.2 Suppose $c$ is one block long, $a$ and $b$ are strings that are a multiple of the block length, and $M(a \parallel c) = M(b \parallel c)$. Here $M$ is CBC-MAC. Then $M(a \parallel d) = M(b \parallel d)$ for any block $d$.
Exercise 6.3 Suppose $a$ and $b$ are both one block long, and suppose the sender MACs $a$, $b$, and $a \parallel b$ with CBC-MAC. An attacker who intercepts the MAC tags for these messages can now forge the MAC for the message $m = b \parallel (M(b) \oplus M(a) \oplus b)$, which the sender never sent. The forged tag for this message is equal to $M(a \parallel b)$, the tag for $a \parallel b$.
Exercise 6.4 Suppose message $a$ is one block long. Suppose that an attacker has received the MAC $t$ for $a$ using CBC-MAC under some random key unknown to the attacker. Explain how to forge the MAC for a two-block message of your choice.
Answer
with the same MAC $t$
Example
$ echo 4d414373206172652076657279207573 | xxd -r -p | openssl enc -aes-256-cbc -e -K 8000000000000000000000000000000000000000000000000000000000000001 -nopad -iv 0 | xxd -p
e8e9a4ce5d20c4adf552b2c6382e124e
$ echo 4d414373206172652076657279207573a5a8e7bd7d41b6c8d524d7b4410e673d | xxd -r -p | openssl enc -aes-256-cbc -e -K 8000000000000000000000000000000000000000000000000000000000000001 -nopad -iv 0 | xxd -p -c 32 | cut -c 33-64
e8e9a4ce5d20c4adf552b2c6382e124e
Exercise 6.5 Using an existing cryptography library, compute the MAC of the message
4D41 4373 2061 7265 2076 6572 7920 7573 MACs are very us
6566 756C 2069 6E20 6372 7970 746F 6772 eful in cryptogr
6170 6879 2120 2020 2020 2020 2020 2020 aphy!using CBC-MAC with AES and the 256-bit key
8000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001Answer
0D82 0E3A 1E10 5D30 7216 FC00 C7A5 B449Solution
$ echo 4d4143732061726520766572792075736566756c20696e2063727970746f677261706879212020202020202020202020 | xxd -r -p | openssl enc -aes-256-cbc -e -K 8000000000000000000000000000000000000000000000000000000000000001 -nopad -iv 0 | xxd -p -c 48 | cut -c 65-96
Exercise 6.6 Using an existing cryptography library, compute the MAC of the message
4D41 4373 2061 7265 2076 6572 7920 7573 MACs are very us
6566 756C 2069 6E20 6372 7970 746F 6772 eful in cryptogr
6170 6879 21 aphy!using HMAC with SHA-256 and the key
0b0b 0b0b 0b0b 0b0b 0b0b 0b0b 0b0b 0b0b
0b0b 0b0b 0b0b 0b0b 0b0b 0b0b 0b0b 0b0bAnswer
BE48 C659 EE04 1EDC 12AF 8D47 9607 7618
9902 E011 B1C6 A540 56A5 B10D 9618 FA4ASolution
$ echo 4d4143732061726520766572792075736566756c20696e2063727970746f67726170687921 | xxd -r -p | openssl dgst -sha256 -mac HMAC -macopt hexkey:0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b
We can verify the answer using the definition of HMAC
m = 4d4143732061726520766572792075736566756c20696e2063727970746f67726170687921
K = 0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b
K' = 0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0b0000000000000000000000000000000000000000000000000000000000000000
ipad = 36363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636
opad = 5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c
K'+ipad = 3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3636363636363636363636363636363636363636363636363636363636363636
K'+opad = 57575757575757575757575757575757575757575757575757575757575757575C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C$ echo 3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D3D36363636363636363636363636363636363636363636363636363636363636364d4143732061726520766572792075736566756c20696e2063727970746f67726170687921 | xxd -r -p | shasum -ba 256
7df010140cf808457a1dd8b0cb4a4a35a8708b77c8a27da4cab9fcb3f839e6f1
$ echo 57575757575757575757575757575757575757575757575757575757575757575C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C5C7df010140cf808457a1dd8b0cb4a4a35a8708b77c8a27da4cab9fcb3f839e6f1 | xxd -r -p | shasum -ba 256
be48c659ee041edc12af8d47960776189902e011b1c6a54056a5b10d9618fa4a
Exercise 6.7 Using an existing cryptography library, compute the MAC of the message
4D41 4373 2061 7265 2076 6572 7920 7573 MACs are very us
6566 756C 2069 6E20 6372 7970 746F 6772 eful in cryptogr
6170 6879 21 aphy!using GMAC with AES and the 256-bit key
8000 0000 0000 0000 0000 0000 0000 0000
0000 0000 0000 0000 0000 0000 0000 0001and the nonce
0000 0000 0000 0000 0000 0001Answer for 128-bit tag
34B0 25A5 7D99 3151 2091 2DEF BFE3 29C3Solution in Groovy
7. The Secure Channel
TODO: Implement secure channel between Alice and Bob in Erlang.
Exercise 7.1 In our design of a secure channel, we said that the message numbers must not repeat. What bad things can happen if the message numbers do repeat?
The same bad things can happen as in Exercise 4.3. Repeating message numbers means reusing the same key stream. Suppose an attacker observes two ciphertexts encoded for the same message number
t1 = 12340000 B24FEDC6243553DA6B1DEF32DCB49FA427A597C2FC806B27BB922940B41C009B25B00106C2F8656089FDAAE017
t2 = 12340000 A743FCDA3E711ECC7D0DFC30CD594ECA8BF27A1DDE276A145CE9BA2AB1C74723881354E667761324DF2446D8F5Since the key streams for both ciphertexts where the same, the attacker can now compute the difference between them
t1 ⊕ t2 = 150C111C1A444D161610130211EDD16EAC57EDDF22A70133E77B936A05DB47B8ADA355E0A58E764456D9EC38E2Suppose the attacker knows the first message and its authentication tag
m1 = 4669727374206D657373616765
a1 = 572DBB8560675858ECC378B2ED4D3767251B4D0431544DFAB26CFE47BCA0752DNow she can compute the second message and its authentication tag
t2 = 5365636F6E6420736563726574 BAFCD529378A877A4BC24B5596DE5D62FE5CF5A99201AD5F3C1ABA11654C4DCF
m2 = 5365636F6E6420736563726574
a2 = BAFCD529378A877A4BC24B5596DE5D62FE5CF5A99201AD5F3C1ABA11654C4DCFExercise 7.3 Modify the algorithms for the secure channel in this chapter to use the dedicated, single-key mode for providing both encryption and authentication. You can use GCM as a black box.
function SendMessage
input: S Secure session state
m Message to be sent
x Additional data to be authenticated
output: t Data to be transmitted to the receiver
assert MsgCntSend < 2^32 - 1
MsgCntSend ← MsgCntSend + 1
i ← MsgCntSend
{C, T} ← AES_256_GCM_128(K, i, x, m)
t ← i || C || T
return t8. Implementation Issues
Standard implementation techniques are entirely inadequate to create secure code.
Unless you are willing to put real effort into developing a secure implementation, there is little point in bothering with cryptography.
Many systems contain so-called optimizations that are useless, counterproductive, or insignificant because they do not optimize those parts of the system that form the bottleneck. We have become quite conservative about optimizations. Usually we don’t bother with them.
There are some programmers who implement assertion checking in development, but switch it off when they ship the product. This is not the security perspective.
Ideally, one programmer implements the module and a second programmer implements the tests. Both work from the functional specification. Any misunderstanding between the two is a clear indication that the specification have to be clarified.
The test code is about as big as the operational code, and we have not found a way fo significantly improving that.
Writing high-quality code takes about as long as writing low-quality code, if you count the time from start to finished product, rather than from start to first buggy version.
9. Generating Randomness
The more you know about a value, the smaller its entropy is.
Estimates of the amount of entropy per character in English text vary a bit, but are in the neighborhood of 1.5–2 bits per letter.
Generate 16 random bytes
dd if=/dev/urandom bs=16 count=1 2> /dev/null | xxd -p
Generate random base64 URL safe encoded string
dd if=/dev/urandom bs=32 count=1 2> /dev/null | base64 | tr "/+=" "_- "
Exercise 9.1 Investigate the random number generators built into three of your favourite programming languages. Would you use these random number generators for cryptographic purposes?
JVM — yes; ERTS — yes; Racket — yes.
Exercise 9.2 Using an existing cryptography library, write a short program that generates a 256-bit AES ket using a cryptographic PRNG.
bin:bin_to_hexstr(crypto:strong_rand_bytes(32)).where bin module is defined here
Exercise 9.5 Using a cryptographic PRNG that outputs a stream of bits, implement a random number generator that outputs random integers in the set $0, 1, …, n-1$ for any $n$ between $1$ and $2^{32}$.
-define(MAX, 16#100000000 - 1).
next(N) when 1 =< N, N =< ?MAX ->
Length = size(binary:encode_unsigned(N)),
Result = binary:decode_unsigned(crypto:strong_rand_bytes(Length)),
if
Result < N -> Result;
true -> next(N)
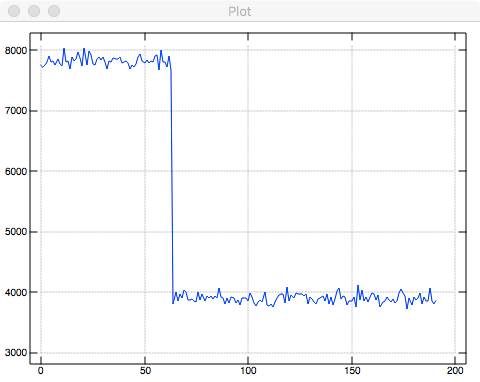
end.Exercise 9.6 Implement a naive approach for generating random numbers in the set 0,1,…,191. For this naive approach, generate a random 8-bit value, interpret that value as an integer, and reduce that value modulo 192. Experimentally generate a large number of random numbers in the set 0,1,…,191 and report on the distribution of results.
load 'plot'
plot #/.~ /:~ 192 | ? 1e6 # 256As expected, small numbers appear as twice as often as large numbers in the set
10. Primes
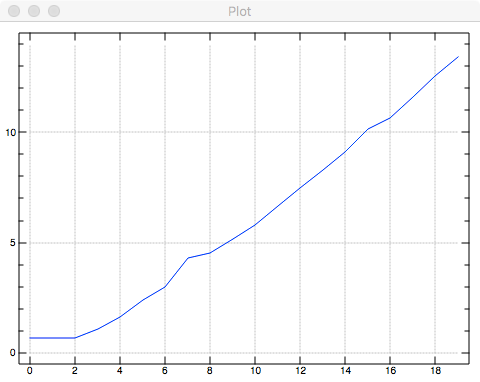
Exercise 10.1 Implement Eratosthenes Sieve. What is the worst-case performance? $O(2^n)$. Generate a graph of the timings for $n=2,4,8,16,…,2^{20}$.
Solution in Erlang.
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 | 131072 | 262144 | 524288 | 1048576 |
| 2 | 2 | 2 | 3 | 5 | 11 | 20 | 73 | 91 | 172 | 335 | 777 | 1729 | 3933 | 9073 | 25632 | 41719 | 108630 | 287291 | 679175 |
Here is the graph in logariphmic scale for $k=1,…,20$.
Exercise 10.2 Compute 13635 + 16060 + 8190 + 21363 (mod 29101) in two ways and verify the equivalence: by reducing modulo 29101 after each addition and by computing the entire sum first and then reducing modulo 29101.
s=: 13635 16060 8190 21363
p=: 29101
1046 = p&|@+/ s
1046 = p&|@(+/) sExercise 10.3 Compute the result of 12358 * 1854 * 14303 (mod 29101) in two ways and verify the equivalence: by reducing modulo 29101 after each multiplication and by computing the entire product first and then reducing modulo 29101.
q=: 12358 1854 14303
p=: 29101
25392 = p&|@*/ q
25392 = p&|@(*/) qExercise 10.4 Is {1,3,4} a subgroup of the multiplicative group of integers modulo 7? No, but {1,2,4} and {1,6} are.
Exercise 10.5 GCD(91261, 117035) = 263.
Exercise 10.6 74$^{-1}$ (mod 167) = 79.
Exercise 10.7 Generate few primes within the range $l=2^{255}$ and $u=2^{256}-1$.
97930216791462598045972883206226108036297956314017330320914377792388523022969
81584374835399266544251931666118226996961716105131490897360674548913013941917
67817200436541682412601222897087873297429605953843518229574841130195287660929
Solution in Erlang
primes:random_prime(maths:pow(2, 255), maths:pow(2, 256) - 1).Long prime
primes:random_prime(maths:pow(2, 2048), maths:pow(2, 2049) - 1).44129837063770165553832059107682306619738412373949690544924694569657334347697318
89282384595223880473291549477607931396621136675427472767457004072458644693312251
85702178678741261775298175549211893240790465679089929528914498139387782873637685
80666645668381134591441541906590131473893822013775159412354495643526549278176367
16420639243316759189536141159464748559796000728199658803151427159954563483308188
14969131978928808655813172004950285866534577393792532435966009786326519840221560
87609143247862022593121169632248770931444531492919464625476888424016012399968184
999766493587299104952314827482039660243903052554035019917
Exercise 10.9 Compute 27$^{35}$ (mod 569).
199 = maths:mod_exp(27, 35, 569).Performed 15 multiplications.
11. Diffie-Hellman
Fermat’s Little Theorem If $p$ is a prime number, then $\forall a \in [1,2,…,p-1] \quad a^{p-1} = 1 \; (\mod p)$.
flt=: | (^~ 1 + i.)@:<:
1 = flt 7Theorem 11.3 $p=2q + 1$, $p$ is a prime number, then $r$ is a square modulo $p$ $\Leftrightarrow$ $r^q = 1 \; (\mod p)$.
Necessity: $r = s^2 \Rightarrow r^q = s^{2q} = s^{p-1} = 1 \; (\mod p)$ by FLT.
Sufficiency: Suppose $\nexists s \in [1,…,p-1]$ such that $r = s^2$. Then $\nexists s \in [1,…,p-1]$ such that $r^q = s^{2q} = s^{p-1} = 1 \; (\mod p)$, which contradicts FLT.
12. RSA
Generate RSA private key using OpenSSL
openssl genrsa -out private.pem 2048
openssl asn1parse -i -in private.pem
The key consists of the follwing components
n :C237C98E92CBABA040C59C5295635D8C143473DDBF64D4A1C26924FC6CE52D98335841764FCEFF577BA650E45E7A6BBB137E4D6098E5C936B0778ED3C7E497287CE10E9645AC1504DEF627D2350F83F7F71269B0C337E7A5DBFE50192FB0475B84F774C208E88CD3C57B8EA3410209C47AE0CD1306B8BA8ACAFBCC9D9547486449FCFC2B779753611012CD405C356F1E6ADFCFFFF96FE853A8CECA1F4F7AF824C20071ED35F46AE50907A826DB3C2E1930BB8B34646BCCE29A8FFC4EE56F59B8A6D038804E12B1064DFEEDDF168DF2456A0B02DE6A8BB07819AACD9DE66D6142B8D93EC557E70DEE77D33DE7342DAD38DFDF1478250C044564D47F176C375D3F
e :010001
d :AC4B475066E3ADC6858F88E52E47AF26648A3FBB995DFECFDDA2DF3FDBEED7AAECE9BF7110CDE6719A6CE9D81E04666BD89834569C6D453A72042E3DAC581ACCBD33FE77CB2924A0649764AE338A271DA41EBE8A243505187B7839608E90C84CE5418D5FD0FD54694E091579B862F17D4F30FC5C839AFF49BF56EFA76055935E703C307855EEDAAB91317AFA74A49086F1BB1D82ED64B6F2420A0416DD05DAB3B2EAE68CE8FFD125CF811422BB833F13F6B72049B150772B0658F720B2226EBFB36146146D45F7A25C2896937682CE4BE849D782A43564B63E5F82E014B767ABDFD0CBC5CDB9096CB8B93B902153B9F2BDEE75A75A644963394F16B2CD5CF4E9
p :EF08538F6BB3A906867EB89D4945478CBB2261F86CA52210A3BD2AE080E6BBCDCF4E37C5C37C5420D9F0D41D4AB93262A181173F79E6A75A8A181268F663843124C09439EB1DE38C3FAE67F3A287112ABFC84B5E7BE4D1DFF09C23AB32A2613012E1C9F964C126595B6F5363D8AD9AF92C7EE3CF44DBCDEC83E7E2D6C012CB4D
q :D001183CFA8C6BDFCD55D5ED247E6566CC3BAA4D0533454A7F1EFD5E9A2D651373D2AF901C18A9480A5EFC5AB0FC533D645BA5027533104D234D15ED7BF3091A99050BA4702E8E52F5E0751960EEE8AEF34FBCF1C53C1BE039335D2063428D0BB728883BFE12BDB68EA8B3C53AFA83F03D86CA6BF188C6907407DEEC2DAA4CBB
d mod (p-1) :C9A991ADCF64ACB687A3C3A75718AEEBA939B1C4000D35772A5D3F1E5741D2B22932C954FCBF18CEFA6FF6D49BA531400B17B900619CDA1645A95766DC704B2796E52E68CAD6D5920E6BDAE1AE7E1B5AA0A0A00D9FA305F9D3AA376188FF7BD52E28F5D8854B7B4A2A1CFB12A2CC9C919A1B97A0D76C460843A4D038F3A52785
d mod (q-1) :7D02EB6A5ABAE26A93A22EFC639E839B10CC1B424709D56F3C8F877FBFF1E0799C76D785291DB93FCEDBDF97321FB47785457F1AC70D7592A6D0C18905A1BFAAF8A48BA6BCB57E5C65E20CFEBFBF56A12F2291504D561EFAD7E602E66041B33B834D1CF3D173BA096A1C024F5B6F0CB4EA85844AF3D35C639D18CDE5EC5C19D9
1/q mod p :C63721E329520C8B40FB881907FD1712C04653D3D6BA84CCC75102444965157311FC08B8D96DF853366B64F1C0698A99DE35157EDA4806E1DB8D21BD45FF1BEDE9E4F69C0FEAA46B828D48C72326FF17C8FFD79EE6A9B204F4C310FF85F825D5EFD042B115CE43A21C1266913A99381A7D3DE12E50C25EB180A25982B16F8432Extract RSA public key from the private key
openssl rsa -in private.pem -pubout
Convert RSA public key between PKIX and PKCS#1 formats
openssl rsa -pubin -in public.pem -RSAPublicKey_out
openssl rsa -RSAPublicKey_in -in pkcs1-public.pem -pubout
RSA implementation in Erlang.
Exercise 12.1 Let p = 89, q = 107, n = pq, a = 3, and b = 5. Find x in $\mathbb{Z}_n$ such that a = x (mod p) and b = x (mod q). Anser: 8458.
3 5 = 89 107 | 8458Exercise 12.2 Let p = 89, q = 107, n = pq, x = 1796, and y = 8931. Compute x + y (mod n) directly. Compute x + y (mod n) using CRT representations. Answer: 1204.
n=: p*q [ q=: 107 [ p=: 89
16 84 = X=: (p,q) | x=: 1796
31 50 = Y=: (p,q) | y=: 8931
47 27 = (p,q) | X + Y
47 27 = (p,q) | n | x + yExercise 12.3 Let p = 89, q = 107, n = pq, x = 1796, and y = 8931. Compute xy (mod n) directly. Compute xy (mod n) using CRT representations. Answer: 3344.
n=: p*q [ q=: 107 [ p=: 89
16 84 = X=: (p,q) | x=: 1796
31 50 = Y=: (p,q) | y=: 8931
51 27 = (p,q) | X * Y
51 27 = (p,q) | n | x * yExercise 12.4 Let p = 83, q = 101, n = pq, and e = 3. Is (n,e) a valid RSA public key? If so, compute the corresponding private RSA key d.
1 = 1 p: 83 101 NB. both primes
1 = 3 +. t=: 82 *. 100 NB. e and t are relative primes
1 = t | 3 * d=: 1367Exercise 12.5 Let p = 79, q = 89, n = pq, and e = 3. Is (n,e) a valid RSA public key? No, because t and e are not relatively prime, d does not exist.
1 = 1 p: 79 89 NB. both primes
1 < 3 +. 78 *. 88 NB. GCD(LCM(79-1,89-1),3) = 3Exercise 12.8 Let p = 71, q = 89, n = pq, and e = 3. First find d: 1027. Then compute the signature on $m_1 = 5416, m_2 = 2397$, and $m_3 = m_1 m_2 (\mod n)$ using the basic RSA operation: 923, 2592, 5086. Show that the third signature is equivalent to the product of the first two signatures.
What does equivalent mean here? $\sigma_1 \sigma_2 (\mod n) = 3834$ is obviously not the same as $\sigma_3$.
{"kty":"RSA", "n":"GK8", "e":"Aw", "d":"BAM", "p":"Rw", "q":"WQ", "dp":"Lw", "dq":"Ow", "qi":"BA"}-----BEGIN RSA PRIVATE KEY-----
MB0CAQACAhivAgEDAgIEAwIBRwIBWQIBLwIBOwIBBA==
-----END RSA PRIVATE KEY-----OpenSSL failed to show it
$ echo '1528' | xxd -r -p | openssl dgst -sha256 -sign my.pem -hex
Error Signing Data
140736496063496:error:04075070:rsa routines:RSA_sign:digest too big for rsa key:rsa_sign.c:122:
13. Introduction to Cryptographic Protocols
The question “Do you trust him?” is incomplete. It should be “Do you trust him with X?”
We talk about trust when we design protocols. Always keep in mind that business people think and talk in terms of risks. You’ll have to convert between the two perspectives if you want to be able to talk to them.
The function of cryptographic protocols is to minimize the amount of trust required.
14. Key Negotiation
Every time a party sends an authentication, the authentication data consist of all the data exchanged so far: all the previous messages, and all the data fields that precede the authentication in the authenticator’s message.
Be very careful with protocol complexity. There are no good modularization notations for protocols, so everything ends up being mixed together.
20. PKI
Create
Create a new key and a self-signed certificate
openssl req -x509 -newkey rsa:2048 -sha256 -keyout key.pem -out certificate.pem -days 730 -subj "/C=CA/ST=Ontario/L=Toronto/O=NDPAR INC./OU=IT/CN=www.ndpar.org"
Inspect
Print first certificate in the file
openssl x509 -in certificate.pem -noout -text
Print specific fields of the certificate
openssl x509 -in certificate.pem -noout -issuer -startdate -enddate
openssl x509 -in certificate.pem -noout -pubkey
Print all certificates in the file using openssl or keytool
openssl crl2pkcs7 -nocrl -certfile certificates.pem | openssl pkcs7 -print_certs -text -noout
keytool -printcert -v -file certificates.pem
Example: Origins of root certificates on macOS 10.12.6
openssl crl2pkcs7 -nocrl -certfile certificates.pem | openssl pkcs7 -print_certs -text -noout | grep 'Issuer:' | grep -oP '(?<=C=)[a-zA-Z]{2}' | tr [a-z] [A-Z] | sort | uniq -c
2 BE, 6 BM (Bermuda), 1 CA, 12 CH, 3 CN, 1 CZ, 6 DE, 1 DK, 1 EE, 4 ES, 4 EU, 3 FI, 4 FR, 5 GB, 1 GR, 1 HK, 2 HU, 1 IE, 6 IL, 1 IT, 4 JP, 1 KR, 3 NL, 2 NO, 4 PL, 1 RO, 2 SE, 2 SK, 1 TR, 4 TW, 63 US, 1 VE (Venezuela)
22. Standards and Patents
The political structure of the committee puts very little emphasis on creating a good technical standard. The most important thing is to reach consensus. The standard is finished when everybody is equally unhappy with the result.
Many standards are internally inconsistent, or even contradict themselves.
For reasons of simplicity and consistency, which are crucial to the overall security, a security system must be designed by a small group of experts.